AutoInt: Automatic Integration for Fast Neural Volume Rendering
Abstract
Numerical integration is a foundational technique in scientific computing and is at the core of many computer vision applications. Among these applications, neural volume rendering has recently been proposed as a new paradigm for view synthesis, achieving photorealistic image quality. However, a fundamental obstacle to making these methods practical is the extreme computational and memory requirements caused by the required volume integrations along the rendered rays during training and inference. Millions of rays, each requiring hundreds of forward passes through a neural network are needed to approximate those integrations with Monte Carlo sampling. Here, we propose automatic integration, a new framework for learning efficient, closed-form solutions to integrals using coordinate-based neural networks. For training, we instantiate the computational graph corresponding to the derivative of the coordinate-based network. The graph is fitted to the signal to integrate. After optimization, we reassemble the graph to obtain a network that represents the antiderivative. By the fundamental theorem of calculus, this enables the calculation of any definite integral in two evaluations of the network. Applying this approach to neural rendering, we improve a tradeoff between rendering speed and image quality: improving render times by greater than 10× with a tradeoff of slightly reduced image quality.
Videos
Technical Video (7 min)
The AutoInt Framework
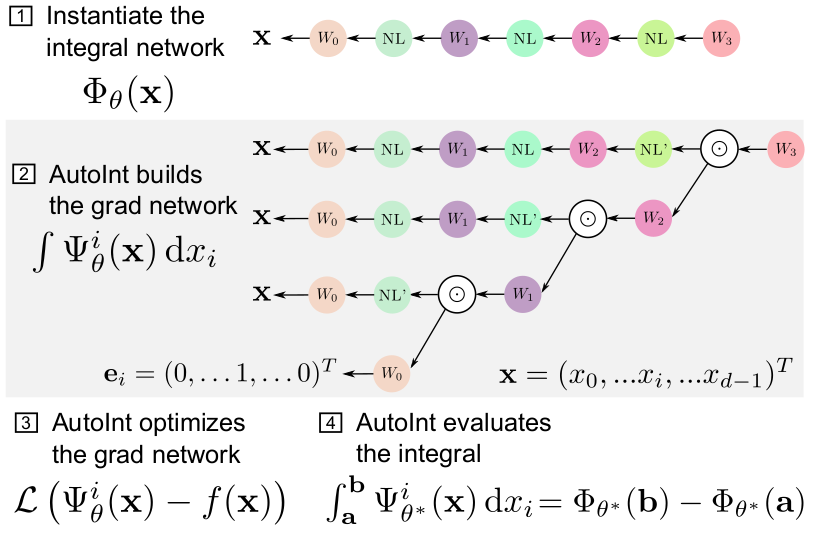
Principle
After (1) defining an integral network architecture, (2) AutoInt builds the corresponding grad
network, which is (3) optimized to represent a function. (4) Definite integrals can then be computed by evaluating the
integral network, which shares parameters with its grad network.
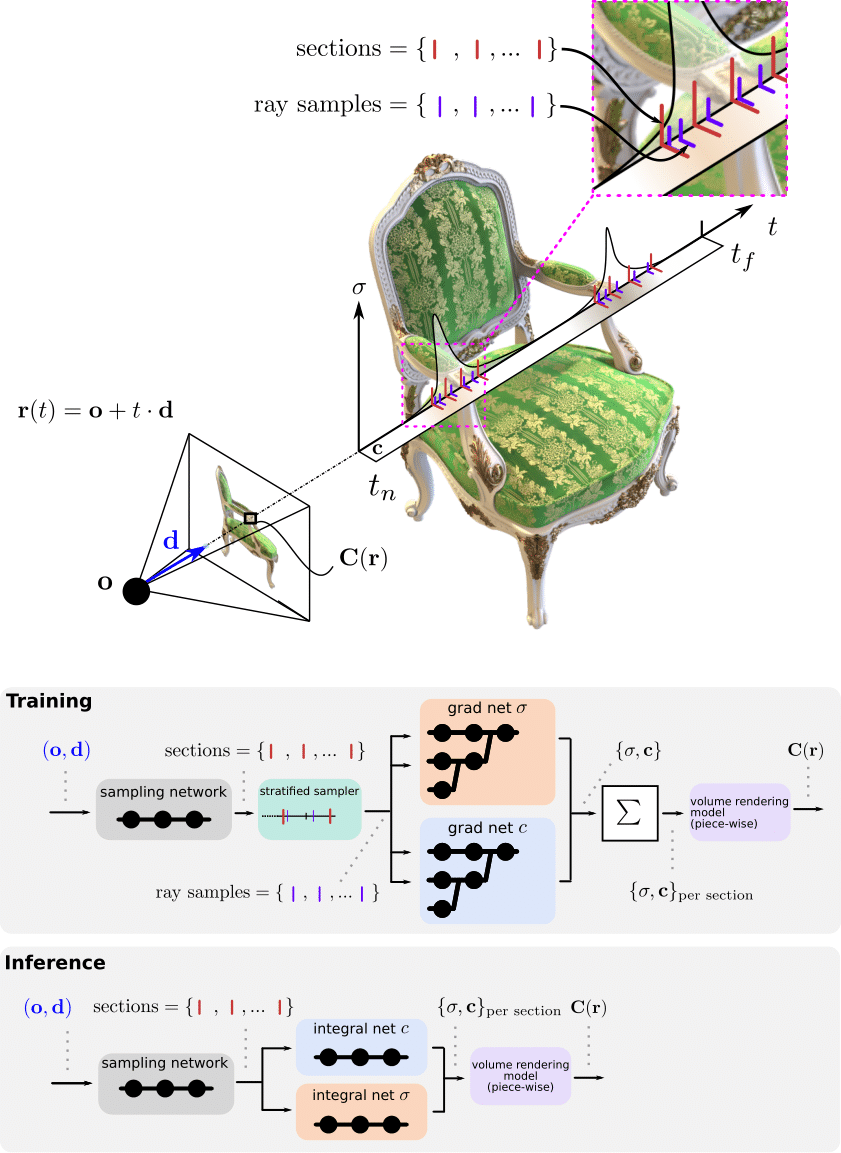
Volume rendering pipeline
During training, the grad networks representing volume density σ and color c are optimized for a given set of multi-view
images (top left). For inference, the grad networks’ parameters are reassembled to form the integral networks,
which represent antiderivatives that can be efficiently evaluated to calculate ray integrals through the volume
(bottom left). A sampling network predicts the locations of piecewise sections used for evaluating the definite
integrals (right).
Results
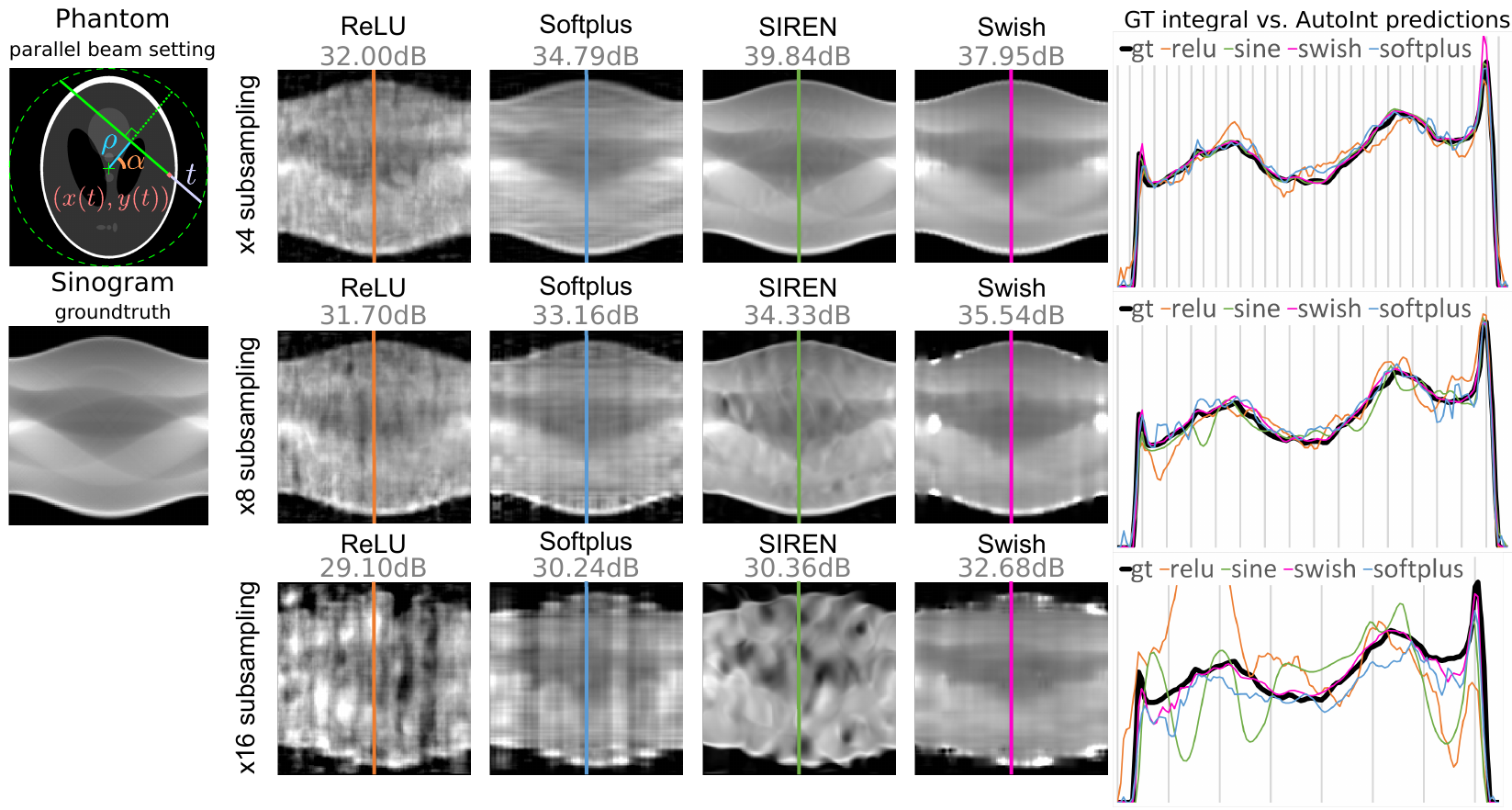
Sparse View Computed Tomography
Left: illustration of the parameterization. Center: sinograms computed with the integral networks using different
nonlinear activation functions. The ground truth (GT) sinogram is subsampled in angle by 4× (top), 8× (middle), and 16×
(bottom). The optimized networks are used to interpolate the missing measurements. Using the Swish activation performs
best in these experiments. Right: 1D scanlines of the sinogram centers shows the interpolation behavior of each method
for each subsampling level.
Volume rendering
On Twitter
Introducing "Automatic Integration (AutoInt)": a new method using neural networks to learn closed-form solutions to integrals.https://t.co/T1qb97h8GC
— David Lindell (@DaveLindell) December 4, 2020
We demonstrate AutoInt for neural volume rendering, achieving >10x speedup compared to NeRF! (1/n)@jnpmartel @GordonWetzstein pic.twitter.com/OOgPzN3pdB