Implicit Neural Representations with Periodic Activation Functions
Abstract
Implicitly defined, continuous, differentiable signal representations parameterized by neural networks have emerged as a powerful paradigm, offering many possible benefits over conventional representations. However, current network architectures for such implicit neural representations are incapable of modeling signals with fine detail, and fail to represent a signal’s spatial and temporal derivatives, despite the fact that these are essential to many physical signals defined implicitly as the solution to partial differential equations. We propose to leverage periodic activation functions for implicit neural representations and demonstrate that these networks, dubbed sinusoidal representation networks or SIREN, are ideally suited for representing complex natural signals and their derivatives. We analyze SIREN activation statistics to propose a principled initialization scheme and demonstrate the representation of images, wavefields, video, sound, and their derivatives. Further, we show how SIREN s can be leveraged to solve challenging boundary value problems, such as particular Eikonal equations (yielding signed distance functions), the Poisson equation, and the Helmholtz and wave equations. Lastly, we combine SIREN with hypernetworks to learn priors over the space of SIREN functions.
Videos
Technical video (10:30 min)
NeurIPS talk (10:30 min)
Using SIRENs to represent signals
Representing images
A Siren that maps 2D pixel coordinates to a color may be used to parameterize images. Here, we supervise Siren directly with ground-truth pixel values. Siren not only fits the image with a 10 dB higher PSNR and in significantly fewer iterations than all baseline architectures, but is also the only MLP that accurately represents the first- and second order derivatives of the image.
Representing audio
A Siren with a single, time-coordinate input and scalar output may parameterize audio signals. Siren is the only network architecture that succeeds in reproducing the audio signal, both for music and human voice.
Ground truth
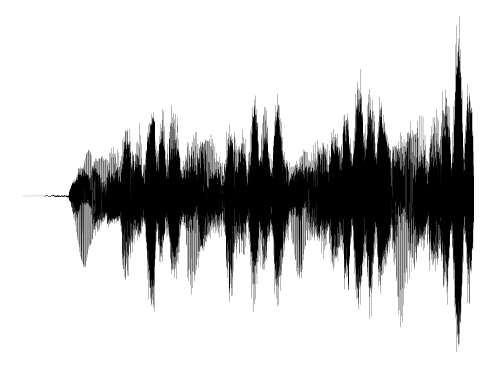
ReLU MLP

ReLU P.E.
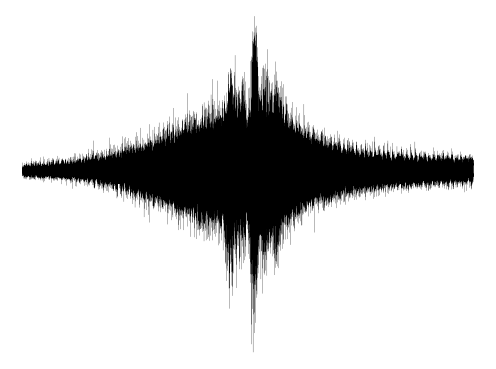
Siren
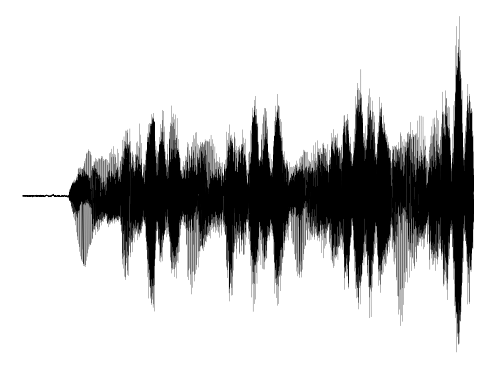
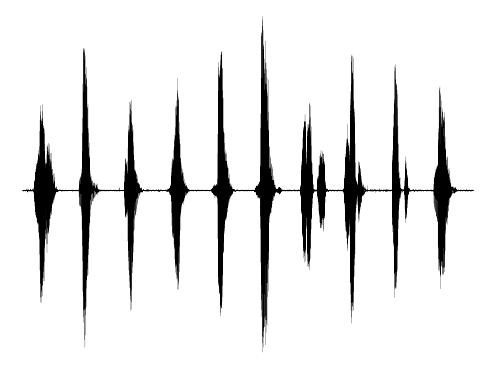

Representing videos
A Siren with pixel coordinates together with a time coordinate can be used to parameterize a video. Here, Siren is directly supervised with the ground-truth pixel values, and parameterizes video significantly better than a ReLU MLP.
Using SIRENs to solve PDEs
Poisson equation
By supervising only the derivatives of Siren, we can solve Poisson’s equation. Siren is again the only architecture that fits image, gradient, and laplacian domains accurately and swiftly.
Eikonal equation: representing shapes
We can recover an SDF from a pointcloud and surface normals by solving the Eikonal equation, a first-order boundary value problem. SIREN can recover a room-scale scene given only its pointcloud and surface normals, accurately reproducing fine detail, in less than an hour of training. In contrast to recent work on combining voxel grids with neural implicit representations, this stores the full scene in the weights of a single, 5-layer neural network, with no 2D or 3D convolutions, and orders of magnitude fewer parameters. Zoom in to compare fine detail! Note that these SDFs are not supervised with ground-truth SDF / occupancy values, but rather, are the result of solving the above Eikonal boundary value problem. This is a significantly harder task, which requires supervision in the gradient domain (see paper). As a result, architectures whose gradients are not well-behaved perform worse than SIREN.
Room - Siren
Room - ReLU
Statue - Siren
Statue - ReLU Pos. Enc.
Statue - ReLU
Hemlmholtz equation
Here, we use Siren to solve the inhomogeneous Helmholtz equation. ReLU- and Tanh-based architectures fail entirely to converge to a solution.
Wave equation
In the time domain, Siren succeeds to solve the wave equation, while a Tanh-based architecture fails to discover the correct solution.
On Twitter
Excited to share our work on "Implicit Neural Representations with Periodic Activations"https://t.co/mSFQIQYcJf
— Vincent Sitzmann (@vincesitzmann) June 18, 2020
We show how to fit complex signals, such as room-scale SDFs, video, & audio, and supervise implicit reps via their gradients to solve boundary value problems! (1/n) pic.twitter.com/5Ob57C4Hqg
A non-linearity that works much better than ReLUs. The work described in this video might also be relevant to understanding grid cells.https://t.co/YlV9j79fgi
— Geoffrey Hinton (@geoffreyhinton) June 18, 2020
Join me on a journey through Implicit Neural Representations 🧠 Here, an entire neural network is dedicated to representing a single image. How? Why? Find out in this video 😉https://t.co/SJUvX7PSfJ@vincesitzmann @jnpmartel @alexwbergman @davelindell @wetzste1 @Stanford pic.twitter.com/W2XE17lF2c
— Yannic Kilcher 🇸🇨 (@ykilcher) June 21, 2020